Three triangles puzzle

May 1, 2020

I stumbled upon this delightful little geometry puzzle on the DataGenetics blog:

There are three identical triangles with bases aligned. If each triangle has an area A, what is the total area of the two regions (B+C) shaded in green?

My solution

My solution relies heavily on finding similar shapes and their scale factors. For clarity, I'm glossing over proving that the shapes I claim are similar actually are, but those details could easily be filled in for rigor.

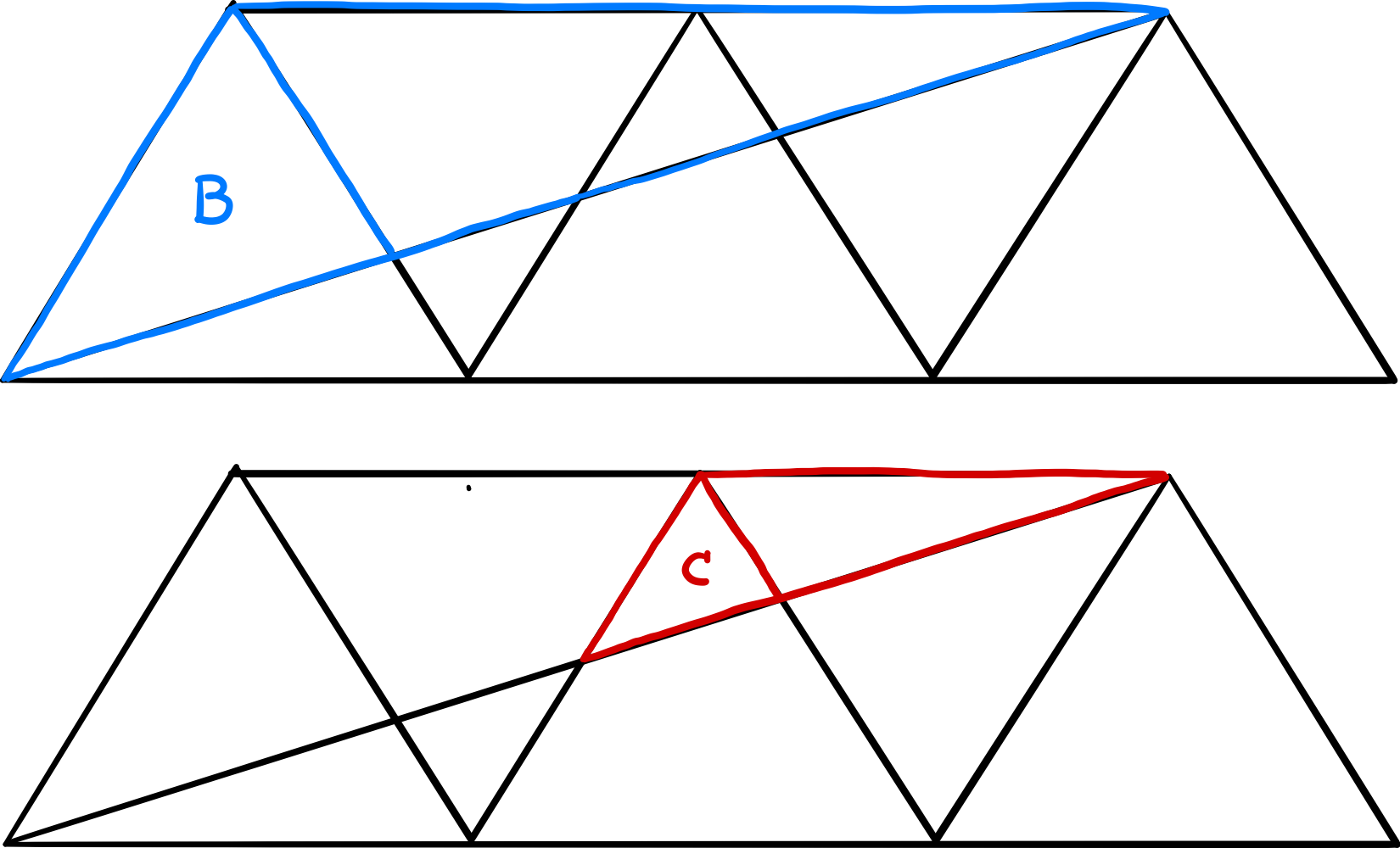
First, we can establish a relation between the areas B and C: In the figure below, where we have added an auxiliary line on the top of the row of the original triangles (or two more similar upside-down triangles, depending on how you choose to look at it), the red and blue shapes are similar. The blue triangle has the upped edge twice as long as the red one, so the scale factor is two. Therefore the area B = 4C.

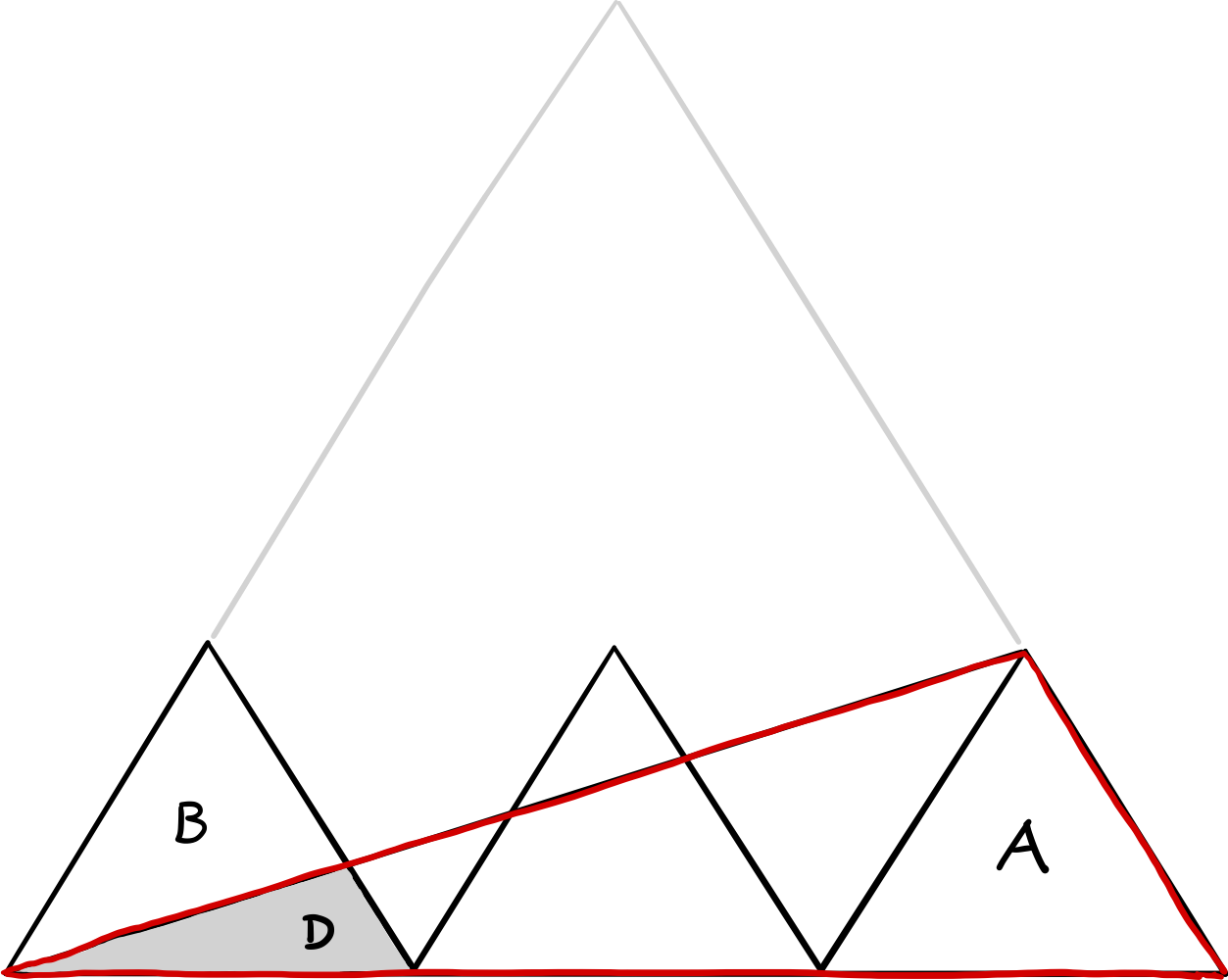
In the next figure, the red triangle has the same altitude as A but the base is three times as long; Therefore its area is 3A. The ratio of the red triangle to the big gray triangle is the same as the ratio D : A, again because of similarity of the shapes. The edges of the big gray triangle are three times those of A, so it has the area 9A. Hence D : A = 3A : 9A = 1 : 3. As B + D = A, that leaves B = 2/3 ⋅ A.

Now that we know that C = 1/4 ⋅ B and B = 2/3 ⋅ A, the rest is simple arithmetic: $$ B + C = \bigg(1 + \frac{1}{4}\bigg) B = \frac{5}{4} B = \frac{5}{4} \cdot \frac{2}{3}A = \frac{5}{6}A. $$